Embrace the Power of Changing Your Mind: Think Like a Bayesian to Make Better Decisions, Part 1

Why Changing Our Minds Matters

Changing your mind is not weakness; it is disciplined strength. We live in a world rewarding certainty, slogans, and quick takes. Yet the choices shaping our careers, finances, health, and relationships usually unfold under uncertainty. The risk is obvious: when we cling to yesterday’s belief in a shifting world, the accuracy of our future judgments drifts away from reality. The result is avoidable regret—missed opportunities, inefficient effort, lower wealth, impaired health, and decisions we cannot defend when the dust settles.

The desire to make good decisions is certainly not new and may seem obvious. So why do we not always make good decisions? It is because we are busy, we love people, we can be a little lazy, and we are creatures of habit.

Psychologists call the stickiness of old beliefs confirmation bias and status-quo bias. Economists observe similar inertia in markets and organizations. Neuroscience adds a critical piece: the brain runs on prediction. When reality surprises us, dopamine spikes signal a prediction error. That signal is a built-in update invitation. Culture and ego often reject it. We rationalize away the signal or drown it out with social proof. Oxytocin is our tribal neurotransmitter, encouraging our focus on people-based decision factors and discounting environmental-based decision factors. Our brain is running an operating system helpful for survival a thousand years ago, but not so helpful today. A better path is to make those error signals actionable through a consistent, repeatable process for belief updating.

This article argues for one simple, powerful habit: treat every important belief as work in progress, not a permanent identity. Test it, update it, and move. The process of keeping those updates honest is called Bayesian inference. Rev. Thomas Bayes did not write a self-help manual. He left us a method for combining prior knowledge with new evidence to form a more accurate belief. That method scales from umbrellas and medical tests to job changes and investment policy.

The point is not to turn life into equations. The point is to install a lightweight belief-updating routine running in the background of daily judgment. When the routine runs, you respond to evidence instead of mood, noise, or pressure. You reduce overreaction to one-off events. You raise your signal-to-noise ratio. You get to be wrong early, not catastrophically late.

This installment lays the foundation. It introduces a words-first version of Bayes’s rule, shows how the pieces interact, then warms up with two examples: an everyday umbrella decision and a gentle medical-testing case. Later installments will add classic puzzles and a full career case study centered on Mia’s job decision, plus a practical playbook for turning updates into action.

Article Series

Over the course of four installments, we will move from foundations to practice, showing how you can strengthen your ability to update beliefs, make confident choices, and better navigate uncertainty.

• Part 1: Foundations of Bayesian Thinking Introduces the belief-updating framework, intuitive examples, and the basic structure of Bayesian inference.

• Part 2: From Intuition to Application Builds from simple examples (like weather forecasts and medical tests) to classic Bayesian puzzles, revealing common errors in reasoning.

• Part 3: Bayesian Inference in Real Life Applies the framework to real-world decisions, with a focus on Mia’s job-change example and how structured updating supports free will.

• Parts 4 & 5: Tools and Exercises for Becoming Bayesian Provides advanced discussion, practical exercises, and a workbook-style appendix with prompts (including “Ask GenAI”) to help you apply Bayesian updating to your own choices.

This journey is about more than math. It is about learning how to embrace uncertainty, change your mind when the evidence calls for it, and make better decisions serving your long-term goals.

Why Is The Belief Updating Framework Necessary

By some estimates, adults make over 30,000 decisions a day. Of course, the vast majority of these are safe, low-impact decisions like, "Should I wear brown or black socks to work?" or "Should I put cream in my coffee?" So the vast majority of our decisions are easily handled by our brain's onboard, default decision systems. The issue is that we are notoriously poor at making the small minority of necessary high-impact decisions. Like "Should I quit my job?" or "Should I own or rent a home?" We naturally try to fit our complex, high-impact decisions into our simple, low-impact, default decision system. They are very different.

The reason we naturally make fast and sometimes inaccurate decisions is simple. Our brain wishes to conserve energy and survive. Our brain learned thousands of years ago: A good survival strategy is to trade accuracy for speed. To demonstrate why this happened, say there are two people, person A and person B, and both are about to get chased by a lion.

• Person A immediately runs as fast as they can in a straight line away from the lion. They did not care about anything other than putting as much distance as possible between themselves and the lion.

• Person B stood still and started calculating the optimal exit route along several different options, considering exit angles, potential obstructions, wind influence, and other factors.

Person A was more likely to escape. Person B became lion food. Since a dead person cannot have children, Person A's "run fast without thinking" genes were passed on to the next generation. Person B's "calculation" genes expired. It is that simple.

Challenges like lion attacks and illness were very common evolutionary survival conditions a thousand years ago. Today, most existential threats have been eliminated by modern medicine and laws. Lions are usually found in zoos, not on the street. So the need for our brain's decision system programmed to trade speed for accuracy is not as necessary. But we still have it.

Today, Bayesian inference is the antidote for our often out-of-date neurobiological decision systems. Once Bayesian inference becomes a habit, you will make faster, energy-conserving, and accurate decisions. But because Bayesian inference is not in our default decision neurosystems, it must be practiced to be habituated. It does not come preinstalled when we are born.

Before we dive into the belief updating framework, let’s clarify the two core ingredients of Bayesian thinking:

EB (Existing Belief):

This is the position you already hold about the world, shaped by your experiences, culture, or intuition. Think of a belief as a mental icon or app: it holds a pre-defined set of instructions running automatically, without conscious deliberation. In this way, beliefs behave much like habits. They serve as mental “easy buttons” streamlining cognition, saving time and energy. The challenge is: Our world is dynamic and ever-changing. A belief once serving you well can become outdated. Anything outdated continuing to run automatically becomes risky—leading you to make poor decisions without realizing it. This makes belief updating so critical.

The Power and Peril of the Habitual Belief

An existing belief (EB) is essentially a cognitive shortcut—a deeply stored sequence of instructions triggered by specific cues. For example, the belief “My industry is stable” is a shortcut automatically instructing you to ignore job-search notices, skip professional development courses, and continue investing only in that sector. This is highly efficient until the underlying reality changes. This system is effective for driving (a set of habitual movements and perceptions) but becomes dangerous for strategic thinking because it prioritizes speed over accuracy. The belief is not seen as a conclusion based on past data, but as a stored identity statement.

As superforecaster and political scientist Philip Tetlock observed, beliefs are properly understood as hypotheses to be tested, not treasures to be guarded.

When we treat an existing belief as a treasure, we are protecting a past success instead of building future resilience. The Bayesian process forces us to downgrade a belief from a certainty to a working hypothesis (A), the critical first step in making it available for revision.

NE (New Evidence): This is fresh information challenging, supporting, or reshaping your existing belief. It can arrive as an observation, a data point, or even a friend’s comment causing you to reconsider.

New Evidence (NE):

In our modern, high-information world, NE is available constantly and in high volume. The problem is not scarcity; it is management. New evidence is rarely a single, dramatic event—it’s a stream of smaller signals, often ignored until they coalesce into a crisis.

Consider the following common types of new evidence frequently going unmanaged:

Existing Belief (EB)	Ignored New Evidence (NE)	Consequence of Neglect
"My client is loyal and will renew their contract."	Consistent slow email response times; a sudden drop in their service usage; your competitor's marketing materials showing up in their office.	Loss of the key client; scrambling to fill a revenue gap visible for months.
"This new investment strategy will perform well, just like the old one."	The strategy’s performance data consistently falling below its benchmark; a respected financial blogger publishing an articulate critique; an unexpected change in regulation.	Significant financial loss; an emotional decision to pull out of the strategy at the worst possible time.
"My current workflow is the most efficient way to work."	Colleagues finishing similar tasks faster; a new piece of software promising automation; repeated small errors appearing in the final output.	Stuck in low-productivity cycle; missing a promotion or being passed over for a leadership role due to inefficient time management.

When new evidence shows up, we need a disciplined way to test how it affects our existing belief. This is where the Belief Updating Framework comes in. We will use it throughout this article series to illustrate how Bayesian inference works in practice.

The Belief Updating Framework

Let us begin with some fundamental definitions about probability and the limits of knowledge, which in turn lead to probability as a way to predict the future.

Probability: The Logic of Uncertainty

Good decisions depend on clear thinking. Because the world is rarely absolute, probability is the logic of uncertainty — a forward-looking framework helping us reason about what might happen next. It reflects how plausible an outcome is given what we know today. Probability is not a physical property of the world but a tool for making informed decisions about the future. Errors are indicated by a lack of accuracy.

The Three Nevers and The Limits to Knowledge

Probability is necessary because of the fundamental informational challenges in complex, real-world systems. These "Three Nevers" define why our knowledge is inherently limited and necessitates a probabilistic, adaptive framework for decision-making.

1. Knowledge is Never Complete

This principle asserts we always operate with partial information, meaning there are inherent and often unknowable blind spots in our understanding of any given situation. A dataset, a historical record, or a current observation can never capture all the relevant variables or hidden intentions. There are always unobserved factors and future contingencies outside the scope of our current knowledge. This reality is famously encapsulated by former U.S. Defense Secretary Donald Rumsfeld's observation: "There are known knowns... but there are also unknown unknowns—the ones we don't know we don't know." It is these crucial unknown unknowns rendering current knowledge inherently incomplete.

Example: Imagine an analyst trying to predict the future price of a stock. The analyst has access to all public data: earnings reports, price movements, and trends. However, the true outcome will be shaped by information the analyst does not know: the CEO is secretly negotiating a major acquisition, or a key competitor is about to announce a revolutionary new product. The stock's future is determined by these crucial, unobserved factors, rendering the prediction flawed.

2. Knowledge is Never Static

This principle highlights two facts: The world is constantly changing, and people are not independent agents. Human agents observe, interpret, and react to changes in their environment, policies, or measurements. This makes knowledge ephemeral and often self-defeating because the very act of measuring or setting a goal for a system changes behavior within it. This dynamism is precisely where Goodhart's Law manifests: "When a measure becomes a target, it ceases to be a good measure." This concept defines an inherent limit to knowledge: the act of observation fundamentally changes the system.

Example: Consider a major financial institution trying to boost performance by setting a strict Key Performance Indicator (KPI): "Every customer must have eight banking products." (The infamous Wells Fargo scandal offers a sharp historical record of this approach.) The executive committee assumes the historical frequency of product adoption reflects stable customer demand. The reactive human dynamism kicks in: bank employees are not independent agents; they react to the new, aggressive target. To meet the quota, employees strategically open unauthorized accounts, sometimes transferring funds without customer consent, and prioritizing quantity over ethical sales. The initial "knowledge" indicating a high product-per-customer frequency equals sales efficiency becomes obsolete and misleading once it is targeted. The underlying goal (true customer service and profitable growth) is subverted by the strategic, interdependent behavior of the people attempting to satisfy the metric.

3. Knowledge is Never Centralized

This principle establishes no single person or institution holds all the relevant information necessary to truly understand a complex system. The crucial knowledge is distributed across countless individuals, organizations, sensors, and locations. This concept is central to the work of F.A. Hayek, who showed how the localized, specific knowledge held by millions of individuals cannot be centrally gathered or processed. This decentralized information is aggregated most effectively through price signals—an action often described by Adam Smith's "Invisible Hand." True insight requires understanding this powerful, distributed reality.

Example: An executive committee at a retail chain decides to aggressively expand its inventory of a new high-tech gadget, "The Zapper." The decision is based on centralized knowledge: favorable reports from the marketing department and high-level sales projections. However, the decentralized knowledge tells a different story: a store manager in a key region knows a local competitor just launched a superior, cheaper alternative; a junior warehouse clerk knows the current racking system can't safely handle the increased volume of The Zapper's large boxes; and the delivery truck driver knows the main shipping route is about to close for two months of roadwork. Because this vital, distributed knowledge isn't efficiently gathered and weighted, the company orders millions of units, only to face immediate, costly problems with collapsing inventory, low sales, and shipping bottlenecks.

The Belief Updating Framework Structure

In complex, dynamic systems, probability guides future expectations. The Three Nevers suggest our knowledge is always incomplete and changing. To bridge the gap between what we know and what might be, we must apply a systematic framework for managing uncertainty.

This is where the Belief Updating Framework comes in. Outside of certainties like death and taxes, all the big decisions shaping our lives—career changes, investments, health choices—operate in the realm of P, or Probability. This framework is the essential tool for managing uncertainty. We will use it throughout this article series to illustrate how Bayesian inference works in practice by treating beliefs as probabilities:

A = Prior belief (P(EB)). Your existing belief and its probabilistic strength.

B = Likelihood (P(NE | EB)). If your belief were true, what is the probability this new evidence would appear?

C = Baseline Evidence (P(NE)). What is the probability this evidence occurs across the whole world of possibilities, not only under your favored belief?

D = Posterior belief (P(EB | NE)). Your revised probability after weighing the prior, the likelihood, and the baseline.

The bar ( | ) separating the probability statements (e.g., P(NE | EB)) is a logic operator meaning "given that" or "conditioned upon."

This operator is fundamental to Bayesian inference because it defines the logical relationship between two events. It tells you the conditional probability—the chances of one event occurring if you assume a second, related event has already occurred.

How It Works

• P(NE | EB) (The Likelihood) is read as: "The probability of the New Evidence, given the Existing Belief."

• P(EB | NE) (the Posterior) is read as: "The probability of my Belief being true, given I have observed the New Evidence."

This is the core logic: it acknowledges when certain things happen (the condition, or "given that" part), it will have a predictable, probabilistic impact upon another thing (the outcome you're measuring). Bayesian inference uses this conditional logic to systematically update your existing belief based on new, specific information.

In words:

Updated Belief = (Existing Belief × Likelihood of Evidence) ÷ Baseline Evidence.

In compact math:

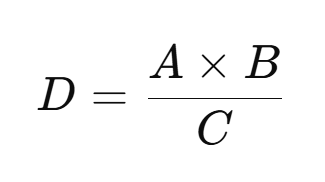
Why these parts?

Each checks a different failure mode:

• A (Prior) counters recency bias by honoring what you already know, while keeping it explicit and adjustable.

• B (Likelihood) asks a directional question: If my belief were true, would this kind of evidence be expected or surprising? (also known as "sensitivity")

• C (Baseline) prevents overreaction to evidence common no matter which belief is true. It is the anchor against sensational anecdotes. (also known as "specificity")

• D (Posterior) is the commitment device—an updated confidence should drive behavior.

The Essence of Belief Updating

The most important lesson about the Belief Updating Framework is that it does not need to be perfect. In fact, it is designed to encourage good over perfect. The act of moving through the framework provides most of the accuracy. The precision of each component—your estimates of the prior, the likelihood, and the baseline—is far less important than the discipline of using the structure.

If you can get each estimate “good enough,” the framework itself will produce a decision more accurate than your intuition alone. The real power lies in making decisions, testing beliefs over time, and allowing yourself to change course when the evidence points elsewhere. Updating is not a flaw. It is life itself. Beliefs are meant to evolve, and the framework provides a systematic way to keep them aligned with reality. When change is in order, you step down a new road with a refreshed belief.

Gradually, Then Suddenly

Belief change rarely feels linear. It often unfolds like a Hemingway character’s fortune. In The Sun Also Rises, a character is asked how he went bankrupt. The reply is simple: “Two ways. Gradually, then suddenly.” Our beliefs behave the same way. We live with a prior for months or years, nudged by small pieces of evidence. The shifts are minor—almost invisible—until new evidence accumulates to a tipping point. What once felt unshakable flips quickly. The Belief Updating Framework lets you track both phases: the gradual drift as probabilities nudge you along, and the sudden shift when the evidence bucket finally tips. Follow the process—prior, likelihood, baseline—and the math works in your favor. Updates accumulate. When the “suddenly” moment arrives, you are prepared, not surprised.

Words Before Math

The essential discipline is to explain A, B, and C in plain language before touching a number. If you jump straight to arithmetic, you risk smuggling in unexamined assumptions.

Words surface the logic:

• Is the prior clear?

• Does the evidence actually fit the belief?

• How common is this evidence in the wider world?

Only after you have articulated these questions should you assign a rough percentage or even a simple category like low, medium, or high. Numbers then refine what words have already been clarified.

Where Neuroscience and Economics Meet Bayes

The framework also reflects how both the brain and markets operate. Neuroscience tells us that the dopamine-based prediction-error system rewards accurate updates. Each time you revise a belief closer to the truth, you strengthen neural pathways, reducing future surprise. In economics, this is equivalent to lowering the transaction costs of making good decisions.

Transaction costs, in this context, are the 'toil and trouble'—the mental effort, time, and stress—spent during the decision-making process.

You also gain from comparative advantage—the key to efficiency.  This means focusing your limited cognitive energy on your unique human strengths. Let tools and calculators handle the arithmetic, data gathering, and record-keeping (the computation). Your role is to frame the question, interpret the context, and weigh values, goals, and risk trade-offs (the judgment). AI fits naturally into this system—it provides structure and computational assistance, while human judgment supplies meaning and direction.

This is the balance of Bayesian thinking: a framework balancing decision process discipline with precision. The Bayesian framework prizes clarity over perfection and adaptability over rigidity.

Common pitfalls Bayes solves

• Priors are Unique and Powerful: This truth is easy to miss - Priors are powerful, often unique, and based on subjective judgment. In the medical case, it is helpful to understand your and your family's history. In more common decisions, like deciding to change jobs, your unique and judgmental criteria for what you want out of the decision are your priors for estimating A.

• Base-rate neglect: ignoring how common the evidence is overall (C). Bayes forces you to compute or at least estimate C.

• Story dominance: a vivid anecdote crowds out quieter base rates. C restores balance.

• Anchoring: the first number or early choice exerts gravitational pull. By making A explicit and then subjecting it to B and C, you weaken the anchor.

• Asymmetric evidence: you overweight signals you “control” and underweight external constraints. Likelihood B asks you to separate agency from environment.

A simple ruler for thresholds

You do not need second-decimal precision. Many decisions improve with three bands and a bias toward action:

• Green (≥70%): continue, compound, or double down.

• Yellow (50–69%): gather targeted evidence, run a pilot, or stage-gate the decision.

• Red (<50%): pivot, pause, or try a safer alternative.

The Umbrella Example: A No-Math Scaffold

Imagine you arrive at an outdoor concert. The morning forecast suggested rain was unlikely. As you step out of your car, you notice dark, fast-moving clouds and a cool gust smelling like rain. You pause and reach for the umbrella in your back seat.

What just happened? You ran a tiny Bayesian update:

• A = Prior belief: “Rain is unlikely.” The forecast anchored you low.

• B = Likelihood: “If rain were coming, clouds like these and the gust would be typical.” High.

• C = Baseline: “Clouds do appear on many dry days.” Moderate.

• D = Posterior: “Rain is likely enough now to change behavior.” You carry the umbrella.

This update did not require numbers. You noticed the fit between the evidence and the rainy-day world (high B). You checked how common similar clouds are even on dry days (non-trivial C). You concluded your belief should increase enough to justify a low-cost action: carry the umbrella. The cost of being wrong is small; the benefit of being right is large. Bayesian thinking pairs naturally with asymmetric payoff logic. Now, math was not required to make the weather decision, especially with the asymmetric payoff logic. If we did do the math, next is how it could turn out, combining our in-the-moment judgments with a past forecast:

The point of sharing the math: Even though the likelihood jumped to 75% because of the clouds and wind, the priors and baseline anchor still keep your Bayesian rain update relatively low, increasing from 10% to 17%. It does not hurt to carry an umbrella, though it is likely you will not need it. Also, from a mental muscle standpoint, practicing and imagining this calculator will help you do it on the fly, especially when the stakes are higher and/or the payoffs are not so asymmetric.

Turn the dial: if the venue offers covered seating nearby, your action threshold rises—you might skip the umbrella. If the event is a long walk from parking with no cover, the threshold falls—you carry it even on weaker evidence. Bayes updates belief; payoffs turn an update into a move.

Why the baseline matters in daily life

Suppose your friend texts, “I hear thunder.” If you live where afternoon storms are frequent, thunder is common (high C), so a single rumble should not swing you to certainty. If you live in a dry climate where thunder is rare (low C), the same rumble carries more weight. Same evidence, different baseline, different update. This is why copying another person’s decision without their context is risky. Their C is not your C.

From words to a quick sketch

When the stakes are higher than umbrellas, jot a fast A/B/C on paper:

• A (Prior): “Given last week’s forecast and season, rain chance low.”

• B (Likelihood): “These clouds and gusts are typical of incoming rain.”

• C (Baseline): “Clouds like this occur often, even without rain.”

• D (Posterior): “Raise rain belief to the ‘carry umbrella’ band.”

This 30-second sketch avoids overreaction to one dramatic cue and underreaction to a meaningful pattern. It also creates a record you can learn from later: was the update too timid or too aggressive? Learning compounds when you leave breadcrumbs.

A Gentle Math Example: Medical Testing Without Panic

Medical testing is where base-rate neglect causes the most pain. A single positive result can trigger fear out of proportion to the true risk. Bayes realigns intuition with reality.

Set-up

• A (Prior): The condition affects 1 in 100 people (1%).

• B (Likelihood): If someone has the condition, the test flags positive 99% of the time.

• C (Baseline): False-positive rate: 5% among healthy people.

• D Question: “Given a positive test, what is the chance I really have the condition?”

Explain the pieces in words first

Prior A tells you rare is rare. Likelihood B says, “If I were sick, a positive test is very expected.” The baseline C asks, “Across everyone tested—sick and healthy—how often does a positive appear?” C matters because a fair number of healthy people will trigger positives by mistake when millions test.

Compute with frequencies, not only percentages

Think in a crowd of 10,000 people:

• Expected to be sick: 1% of 10,000 = 100 people.

• Of those 100, true positives at 99% ≈ 99.

• Expected to be healthy: 9,900 people.

• Of those 9,900, false positives at 5% ≈ 495.

• Total positive tests ≈ 99 + 495 = 594.

Now update: among 594 positives, about 99 are true cases. Posterior D ≈ 99/594 ≈ 16.7%. The test increased belief dramatically (from 1% to ~17%) but did not make the belief certain. Next steps—confirmatory tests, clinical judgment, and context—make sense.

Write the formula transparently

• A = P(EB) = 1%

• B = P(NE | EB) = 99%

• C = P(NE) = (1% × 99%) + (99% × 5%) = .99% + 4.95% = 5.94%

• D = P(EB | NE) = (A × B) ÷ C = .99% ÷ 5.94% ≈ 16.7%

Do you want to try it yourself? Please use the calculator by moving the slider to the estimated probabilities:

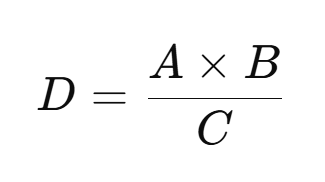
Managing Information and Incentives

The Bayesian approach is not only about how you handle numbers—it is also about how you handle who provides the numbers. Every piece of evidence comes from somewhere, and those sources often carry their own incentives. Doctors, hospitals, insurers, pharmaceutical companies, and government programs all operate within economic systems rewarding certain behaviors.

This does not mean the American medical system cannot be trusted. It means the system can be trusted to follow its incentives—and those incentives are not always aligned with your well-being. I do find this incentive misalignment to cause many people annoyance and to be judgmental. Such as "I'm paying their salary, so why the heck are they not looking more after my needs than following their own incentives!" I hear you. They are looking after your needs in a way aligned with their own incentives and constraints. It is tricky. The day you become less judgmental and more accepting of the system's nature to follow its incentives is the day you will become a much better decision-maker.

Even with those reward incentives, medical people will rarely lie, also known as an error of commission. Lying is certainly against the medical code of conduct, the Hippocratic oath, and many laws. It is more likely they will only tell you the part of the truth aligned with their incentives and be silent on information inconsistent with those incentives - known as an error of omission. By the way, do not be mad at the doctor or nurse. They are only following their training. They often have "standard operating procedures" or "SOPs" which reduce judgment and reinforce medical business incentives. SOPs are part of a business's operating system, especially in large business systems like hospital networks or large medical insurers. SOPs are how they maintain business discipline, provide consistent service, and provide expected returns to shareholders. Sounds good! Unless you are patient in need of the judgmental expertise of an experienced medical practitioner.

A doctor and/or an insurance company may have an SOP suggesting:

If a test result is"X," then the billable procedure is "Y."

For example:

• Test Result (X): Magnetic Resonance Imaging (MRI) reveals a herniated disc (bulging disc) or disc degeneration in a patient with chronic lower back pain.

• Standard Billable Procedure (Y): The insurance company's SOP approves payment for a microdiscectomy (surgery) to remove the portion of the disc that is pressing on the nerve.

• The better, non-surgical alternative (Z): For most patients with chronic lower back pain, even those with MRI abnormalities, the recommended initial treatment is prolonged conservative care, such as physical therapy, pain management, and therapeutic exercise. Studies show that for many people, conservative care is as effective as surgery in the long term.

"Y" is what the insurer will pay for without any discussion. It is the doctor's easy button. But what if the non-surgical option "Z" is a better procedure alternative? However, the doctor's incentives align with "Y" and the insurance company allows it, so a slam dunk for the medical practice. Technically, "Y" is not wrong and the SOP provides the doctor with plausible deniability if questions arise. Even though "Z" is better, but provides less revenue to the doctor. The doctor's incentives point them toward "Y" - an error of omission compared to "Z." Over time, the doctor's training will steer them away from even considering "Z" for other patients. The SOP reduces judgment. Ironically, if a doctor's job is to follow the SOPs, then it makes one wonder the value of paying a higher fee for a doctor. Why not just have an AI read the test results and cut out the middleman!

Obviously, errors of omission can be dangerous in a medical decision. If someone has procedure "Y" and they die, "Z" clearly should have been considered. Without asking the right questions, the patient may have never known "Z" was a worthy decision alternative. The Bayesian lens and a structured decision process give you a way to be your own decision advocate by asking:

• Have my priors been properly considered?

• What assumptions underlie the information I’ve been given?

• What incentives might be shaping how this guidance is presented?

• Should I dig deeper to validate the evidence before acting on it?

• How will a second opinion help to uncover errors of omission?

By explicitly testing priors, likelihoods, and baselines, you can make stronger decisions in a landscape where conflicts of interest are real. This does not replace medical expertise, but it makes you an active participant in filtering, questioning, and refining the evidence presented to you.

Why This Matters for Decisions

First, it prevents panic. A positive test moves you from “rare” to “possible,” not to “certain.” Second, it encourages the right next action: follow-up testing with a more specific method, or retesting to rule out lab error. Third, it reminds both clinicians and patients to consider pre-test probability—the prior (A), based on symptoms, exposure, and local prevalence—before interpreting a result.

How Changes in A, B, or C Shift the Outcome

• Adjusting your prior (A): Though the average condition affects 1% of people, you have led a very healthy life, are in good shape, and have no history of this condition in your family. This means your individual prior can be decreased from 1% to 0.25%. If B and C remain constant, the Posterior (D) drops significantly from 16.7% to 4.73%. This illustrates how factoring in personal context and a lower, personalized prior dramatically impacts the final revised belief.

• Better specificity (lower false positives in C): If the false-positive rate drops from 5% to 1%, total positives shrink and the positive predictive value rises, even with the same A and B.

• Lower sensitivity (B): If the test misses more true cases, a negative result is less reassuring, and the screening strategy must adapt.

Adjusting the probabilities is known as sensitivity analysis. It helps you make change decisions when the world changes. Also, it helps you understand the power of small changes to the probabilities. My advice: do not drive yourself crazy by overthinking your initial decision. Rather, gather information, apply your judgment, and determine your starting posterior (D). If there is additional helpful but unavailable information, make a note of it. Then walk away from the decision for a day or so. Upon returning, use our Bayesian inference framework to ask good questions, gather additional information, and fine-tune your posterior to determine the best decision. Please be confident: This process will help you make an accurate decision even if the exact probabilities are not as precise as you wish they were. There is always more information, even though more information is not always necessary to make a good decision. Do not let yourself get bogged down.

The Bayesian approach helps you answer these questions:

1. Should we do nothing or change?

2. If change is not an option, how should we change?

Turning Bayes into Patient-Friendly Language

“You tested positive. Given how rare this condition usually is and how the test behaves, your chance is roughly one in six, not near certainty. The next step is a confirmatory test with fewer false positives. We will also weigh your symptoms and exposure to adjust the prior up or down. The goal is to move from one in six toward either much lower or much higher before making a treatment decision.”

A micro-checklist for any test or screen

1. What is the base rate (A) in my setting?

2. How expected is this evidence if the condition were present (B)?

3. How common is the evidence overall (C), including false alarms?

4. What action fits the updated belief (D): watchful waiting, confirmatory testing, or treatment?

5. What is the payoff asymmetry if I act now versus wait?

Practical notes for leaders and analysts

• Replace “significant” with “useful.” A statistically significant blip may be common noise (high C). Ask how the signal changes behavior given payoffs.

• Visualize frequency trees. People grasp counts faster than conditional percentages.

• Separate estimation from decision. Estimation updates D; decision integrates D with costs, benefits, and timing.

Deepening the Baseline (C): a closer look

Baseline Evidence (C) is the least intuitive step because we prefer stories to statistics. A vivid anecdote feels rare even when it is common, and our attention confuses “memorable” with “meaningful.” To tame this bias, translate the evidence into a world of many trials. Ask: “If I watched 100, 1,000, or 10,000 runs, how often would I see this evidence—regardless of which belief is true?” This large-numbers frame shows whether the evidence is a black swan or a backyard pigeon. Outliers remain, but the frame keeps us from overreacting to them.

Here is where mathematical intuition matters. Because Baseline Evidence sits in the denominator, it acts like a lever on how much your Prior Belief (A) and the Likelihood of the New Evidence (B) transfer into your Posterior Belief (D).

• If the Baseline Evidence probability is high and stable, the lever is steady. Your Posterior Belief mostly reflects the straightforward interaction of your prior and the likelihood.

• But if the Baseline Evidence probability is low—or falls sharply—the lever shifts. Suddenly, the same prior and likelihood produce a much larger swing in your posterior. In this case, the rarity of the evidence magnifies the update, sometimes dramatically so.

The lesson: Baseline Evidence tells you when to update cautiously and when to update boldly. If the evidence appears often across multiple explanations, it is a weak discriminator—you should move slowly. If it appears rarely except under your belief, it is a strong discriminator—you should move decisively.

Three micro-exercises to build intuition

1. Hiring signal. A candidate arrives with a glowing reference. A: Your belief the candidate will succeed based on the rest of the packet. B: If the candidate is excellent, references like this are common. C: Glowing references are also common for average candidates. D: Do not over-update unless the reference speaks to unique, job-critical behavior with examples.

2. Investment headline. A stock jumps 5% on “breakthrough news.” A: Your belief about the firm’s long-run earnings power. B: If true breakthroughs occur, a jump is expected. C: Headlines labeled “breakthrough” appear weekly across the market; most do not change the base trajectory. D: Unless A was already high, you log the news, not chase it.

3. Health habit. A single week of perfect sleep and diet makes you feel amazing. A: You believe the habit shift helps. B: If the habit works, feeling great is expected. C: Short streaks often occur due to noise (lighter calendar, seasonal mood). D: Extend the trial to four weeks before major conclusions.

Quantifying without numbers

Sometimes numbers exist but do not transfer well to your case. In those moments, use coarse bands:

• A (Prior): low/medium/high confidence.

• B (Likelihood): evidence looks off-brand /neutral/on-brand for the belief.

• C (Baseline): rare/occasional/common in your environment.

• D (Posterior): move down a band/hold/move up a band.

This coarse update is superior to no update. It keeps you honest about direction even when precision is unavailable. Later, when better data arrives, you can refine the bands into percentages.

Payoff asymmetry: why updates are not the whole story

Bayes estimates belief. Decisions blend belief with payoffs and timing. A small belief increase can still justify action when upside dominates downside. Conversely, a large belief increase can wait if the option value of delay is high. Two quick examples:

• Umbrella again: costs little to carry, saves a drenched evening. Act on modest belief.

• Surgery decision: even with a high belief in benefit, you may stage more diagnostics if the procedure carries serious risk. You harvest option value by delaying until information improves.

Ethical guardrails for updates

• Steel-man the other side. Before updating, state the best case for the belief you oppose. If your update survives the test, it is more credible.

• Separate observation from judgment. Record what happened, then interpret. Do not let labels pre-color the facts.

• Disclose uncertainty when others rely on your conclusion. “Here is my updated view and what would change it.” Intellectual humility builds trust.

A one-page template you can photocopy

Belief: _____________________________Purpose of decision: __________________Date: __________ Next review: ________

A — Prior (P(EB)):

Why this prior makes sense: _________________________________________

Confidence band (Low/Med/High): ____

B — Likelihood (P(NE | EB)):

Why this evidence fits or clashes: ___________________________________

Band (Off-brand/Neutral/On-brand): ____

C — Baseline (P(NE)):

How common is this evidence broadly? ________________________________

Band (Rare/Occasional/Common): ____

D — Posterior (P(EB | NE)):

Direction (Down/Hold/Up): ____

New band: ____

Action linked to band: ______________________________________________

Next trigger to revisit (time or event): ___________________________

Build culture around updates

If you lead a team, normalize updates. Hold a monthly “belief review” where you pick two core assumptions and run the A/B/C/D cycle out loud. Reward clean revisions over stubborn consistency. Create a small trophy for the “Best Update of the Month.” Gamify humility. Over time, your team will ship better products, exit dead ends sooner, and trust one another more because they see how decisions evolve.

A closing thought for Part 1

The essence of belief updating is not perfection—it is disciplined adaptability. The framework does not demand exact numbers or flawless calculations. It demands you pause, clarify your priors, test evidence against them, and recognize when change is needed. Good enough is powerful enough. By making decisions, testing them, and updating over time, you grow more accurate and more resilient.

Bayesian updating is not a parlor trick. It is a way to respect what you know, listen to what the world tells you next, and translate the combination into behavior. When you practice on umbrellas and lab tests, you train a reflex you can rely on when the stakes rise.

In Part 2, we will stress-test the framework against counterintuitive puzzles, then apply it to a consequential career decision where emotions run high and the costs of waiting are real.

Resources for the Curious

• Reill, Amanda. "A Simple Way to Make Better Decisions," Harvard Business Review 2023.

• Bastiat, Frédéric. That Which Is Seen, and That Which Is Not Seen. Originally published 1850.

• Box, George E.P. Empirical Model-Building and Response Surfaces. Wiley, 1987.

• Dalio, Ray. Principles: Life and Work. Simon & Schuster, 2017.

• Dweck, Carol. Mindset: The New Psychology of Success. Random House, 2006.

• Epictetus. Enchiridion. 125 CE.

• Goodhart, Charles A.E. "Problems of Monetary Management: The UK Experience." In Papers in Monetary Economics, Volume I. Reserve Bank of Australia, 1975.

• Hayek, F. A. “The Pretence of Knowledge.” Nobel Prize Lecture, 1974.

• Hemingway, Ernest. The Sun Also Rises. Charles Scribner’s Sons, 1926.

• Jaynes, E. T. Probability Theory: The Logic of Science. Cambridge University Press, 2003.

• Kahneman, Daniel. Thinking, Fast and Slow. Farrar, Straus and Giroux, 2011.

• Rumsfeld, Donald. Known and Unknown: A Memoir. Sentinel, 2011.

• Sapolsky, Robert. Determined: A Science of Life Without Free Will. Penguin Press, 2023.

• Tetlock, Philip, and Dan Gardner. Superforecasting: The Art and Science of Prediction. Crown, 2015.

Jeff Hulett’s Related Articles:

• Hulett, Jeff. “Challenging Our Beliefs: Expressing our free will and how to be Bayesian in our day-to-day life.” The Curiosity Vine, 2023.

• Hulett, Jeff. “Changing Our Mind.” The Curiosity Vine, 2023.

• Hulett, Jeff. “Nurture Your Numbers: Learning the language of data is your Information Age superpower.” The Curiosity Vine, 2023.

• Hulett, Jeff. “How To Overcome The AI: Making the best decisions in our data-saturated world.” The Curiosity Vine, 2023.

• Hulett, Jeff. “Our World in Data, Our Reality in Moments.” The Curiosity Vine, 2023.

• Hulett, Jeff. “Solving the Decision-Making Crisis: Making the most of our free will.” The Curiosity Vine, 2023.

• Hulett, Jeff. Making Choices, Making Money: Your Guide to Making Confident Financial Decisions. Definitive Choice, 2022.